Waves in random media and time reversal

We studied the diffusive behavior and energy equilibration in a randome elastic media. Developed the sparse matrix canonical grid method to deal with large-scale systems. We also investigated the imaging through complex media and explored the resolution limit.

Details

Random media exist everywhere in nature. In a random medium, wave propagation exhibits interesting behaviors such as diffusion and localization that can be described by either physics models or statistics models. For elastic waves traveling in random media, the compressional and shear energy will reach an equilibrium status after sufficient number of scatterings. However, when the scattering is very strong and the near-field effect becomes significant, the energy ratio may differ from the value given by the equipartition principle. This might have the application in seismic modeling.

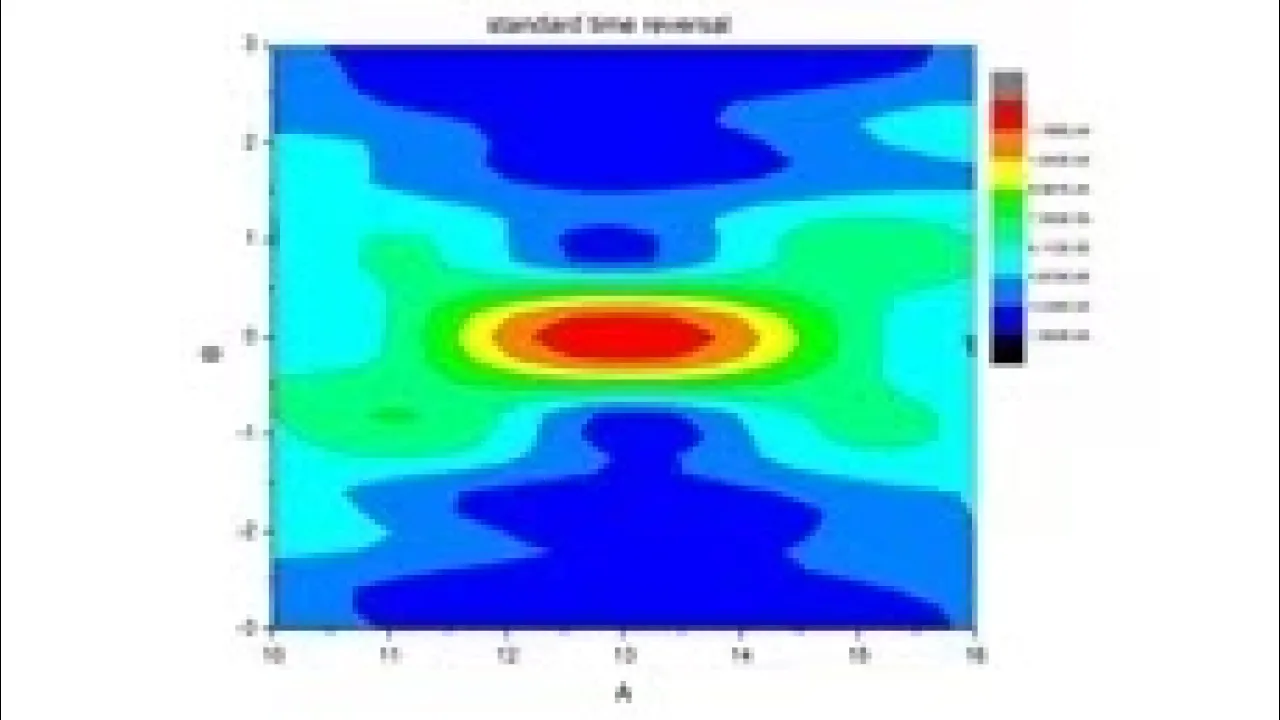
Time reversal refers to the following physical process: the source emits signal, the signal propagates in a medium and be recorded by an array of transducers. Then the transducers reverse the signal and send it back into the original medium. Because of the time-reversal invariant of the wave equation, the signal will travel back and refocus at the source position. Imaging is very similar to time-reversal, but the back propagating medium is a fictitious medium. We used the T-matrix method and take all the multiple-scatterings between any two scatterers to do numerical time-reversal and imaging through strong-scattering random media. This is not only physically interesting but also numerical challenging.

Collaborators

Prof. George Papanicolaou, Mr. Pierre-David Letourneau

Waves in random media and time reversal

Share

Waves in Complex Media (WCM)